In the pursuit of a complete model for human reasoning, one task which is crucial to the final product is an effective model of reasoning. The ability to combine known facts in order to create new facts is a process humans do effortlessly in our daily lives. When critically applied, the process of producing new facts from existing information helps to forward most, if not every, human endeavor. Modeling this process has, consequently, been attempted and refined many times.
An aside on logical variables and notation:
Propositional Logic Terminology:
| Term | Meaning |
| x | x is true |
| ~x | x is false |
| x ∧ y | x and y are true |
| x → y | If x is true then y is true |
One approach to producing new facts from old ones is binary propositional logic. Propositional logic allows us to capture relations between statements about the world. Say we have three propositions: “the temperature is below 32 degrees” (t), “there is precipitation” (p), and “it is snowing” (s). From these variables we can make a few statements about the relationship between them: “if t and p are true, then s is true” (t ∧ p → s), “if t is false then s is false” (~t → ~s), and “if p is false then s is false” (~p → ~s). These rules let us use limited information we might have to gain more information about the state of the world. Say we know that it’s snowing. From that information and these rules, we can figure out both that it is below 32 degrees and that there is precipitation.
Bayesian reasoning terminology:
| Term | Meaning |
| P( A ) | The probability of A being true |
| P( ~A ) | The probability of A being false |
| P( A, B ) | The probability of A being true and B being true |
| P( A | B ) | The probability of A being true in the context that we know B is true |
A alternative method for modeling reasoning is Bayesian probability, which, like propositional logic, consists of beliefs and relations between beliefs. The major benefit to bayesian networks over classical logical networks is that, rather than the beliefs and relations being binary, they are probabilistic. This helps immensely, because, outside of the frictionless vacuum that is classical logic, most events and relations between events aren’t known with 100% certainty. Where a classical interpretation of the model above would be easily disprovable with a counterexample (say… hail?), the bayesian interpretation (annotated below) is far more robust.
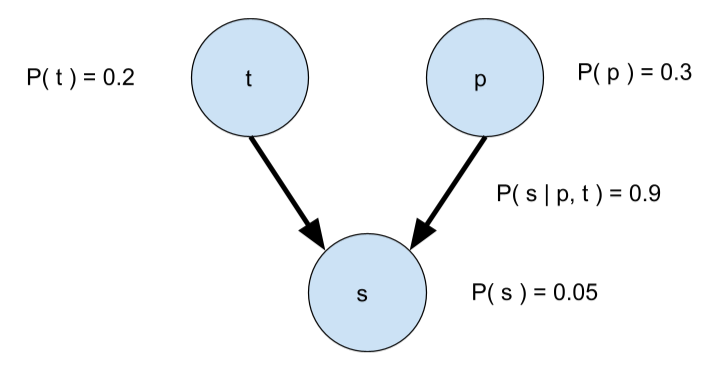
In dealing with probabilistic events rather than binary facts, Bayesian models capture the incomplete knowledge that we hold about the world. Most statements humans make are collectively understood to be mostly true, but sometimes false. When I say that the bus arrives at 8, nobody would claim I’m a liar if the bus didn’t come one day. My statement clearly isn’t meant to mean that it would be impossible for the bus not to come at 8, but rather that I intend the listener to believe that the bus will arrive at 8. I hold some internal high probability of the bus arriving at 8 (like 99%), and make statements to bring the listener’s probability close to mine. For this reason, taking statements about the world and feeding them into a binary logic machine would in surprisingly often produce unexpected and intractable paradoxes when unlikely scenarios occur that counter the statements programmed into it. By storing probabilities rather than binary facts, the model can recognize when an unlikely but possible event occurs and reason through it.
Even if we did prefer the binary format for facts in terms of communicating information to the person running the inference machine, we could always write rules to convert probabilities into binary facts, whereas we couldn’t do the same in reverse order. We could tell the program to convey knowledge it holds at greater than 95% likely as true, and knowledge it holds at less than 5% likely as false, leaving everything in the middle as so far undecided. That would allow the machine to reason internally with probabilities, but convey knowledge externally as facts. We cannot convert the other way around, because there are only two values in classical logic to project onto a continuous range between probabilities zero and one. If you set every false statement to probability 0 and every true statement to probability 1, you would get a working bayesian network that produces the same results as your binary network, but it would be similarly stuck saying all statements are 100% true or 100% false. Probabilistic models of reasoning are more expressive than binary models in capturing systems of imperfect knowledge.
Next week! The math behind Bayesian reasoning.